string simulator physics and mathematics
by
Theo Verelst
(Last update Oct 6, 2006)
Introduction
I've made a string simulator which is a program running on a fast PC or
unix workstation to simulate the motion of strings in a musical
instrument, based on a physical model of a vibrating string. A string
like on a guitar or even in a piano is suspended between two fixed
points, which are to begin with thought to be unmoving, and is though
to be brought into a natural motion by displacing it, thus straining
it, and then releasing the virtual string, computing how it will move.
From the computed motion, a sound can be derived, which is made audible
through a computer sound device. To make the sound more interesting and
the motion more complex to understand and predict, more than one string
can be sounded at the same time and coupled to eachother.
See also the program
oriented page about the actual software computing the simulaneous
motion of up to 10 strings (on a very fast machine), of which a live
demonstration has been
presented at FOSDEM conference at brussels university, the
demonstration audio files and open source software files are on the web.
The suspended string
A string in this case is considered to be a thin stretch of metal which
is under tension and with fixed supports on both ends, and which is
free to move, to begin with only in two dimensions, such that excursion
from the rest condition (where the string is without counting gravity a
straight line) is a scalar, not a vector.

A
string in motion, suspended on fixed points at its ends.
The string has a finite weigth and a known length and moves after is is
exited by striking it or plucking it, or in mathematical physical sense
giving it an initial state unequal to the rest state, and is assumed to
move according to the newtonian and basic equations of motion.
Because there are no easy closed form solutions to the evolution of the
string state starting from a random initial state, I use an
approximation, a model of the problem, where the string is like in
finite element analysis cut up in pieces (order of magnitude: 10^2) of
equal weight which all follow the 2d order equtions of motion,
preferably inintegral form, and connect together over elastically
behaving string segments.
A single harmonic oscillator as string section
Consider one of the harmonic oscillator sections of the cut-up string:
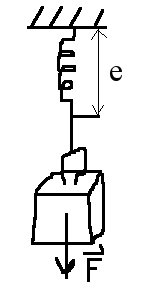
The Harmonic swing with excursion e.
Gravity would excert a force F
= g . M , where M is the mass of the weight, just like the
spring will excert a force in the other direction on the weight,
depending on how much the spring is chaged, proportional to the
excursion e.
Commonly known this system will oscillate as a perfect sine wave when
exited and when there is no friction or interaction with other systems.
The piece of string weight in this case is hung from a fixed mass, the
ceiling or so, which doesn't move or influence the oscillation.
The string as coupled harmonic oscillators
To simulation the motion of the whole string, a little piece of metal
from the string is considered to represent a fraction of the weigth of
the string and is considered connected to the adjacent pieces of weight
of the string and the string length is taken to be madeof an equal
number of little springs, which connect the weight fractions together:
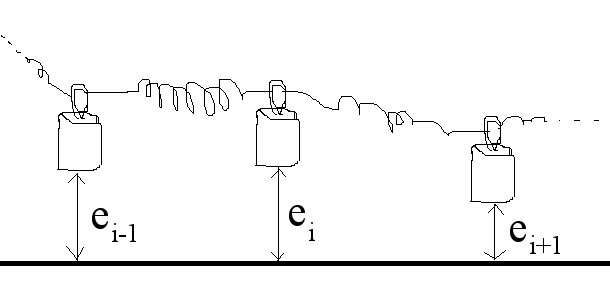
so as to form a set of connected or coupled harmonic oscillators with
floating suspension points.
At any point along the string, there is a force acting upon the weight
concentrated in that point which is the sum of the two forces from the
neighbouring points, which are the products of the string constants and
the displacement differences, including the signs.
For each mass concentration point, all with equal weights, the well
known Newtonian equations of motion hold, the velocity is the integral
of the force acting on the particle per time interval, the displacement
is the integral of the velocity at any point in time. And to make the
local harmonic oscillator work, the springs excert a force proprtional
and opposite to the displacement with respect to local equilibrium.
For a small integration approximation step size, one could take a
linearisation, and perform simple additions to compute the integrals of
velocity and displacement.
To do this integration approximation over all the string segments aka
mass concentration points, a sweep over all segments is done in a fixed
direction over all the points. Since accuracy is a big problem, because
a hundred coupled harmonic oscillatlors generate a lot of total
rounding noise, the practical real-time simulation uses a normalisation
which requires no multiplications, so no rounding errors of the
rational kind are made at each sweep step.
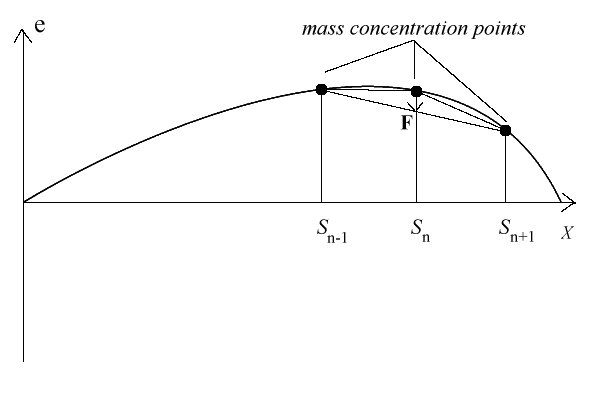
String damping, lossyness
A natural string always experiences damping, both from air friction and
from internal friction in the string and at the end points, related to
the clamping of the material and the suspension point material. As a
result the sound of the string decays with time, and also the tonal
quality changed with time, and by and large gets duller after a while.
To make the string damped a bit, so that it sounds softer (and
different) after a while, the end points are considered a bit stiff and
a bit damped. This in the practical simulation is done by forcing the
excursion down around the end points, gradually increasing the
forcedown toward complete damping at the two string suspension points.
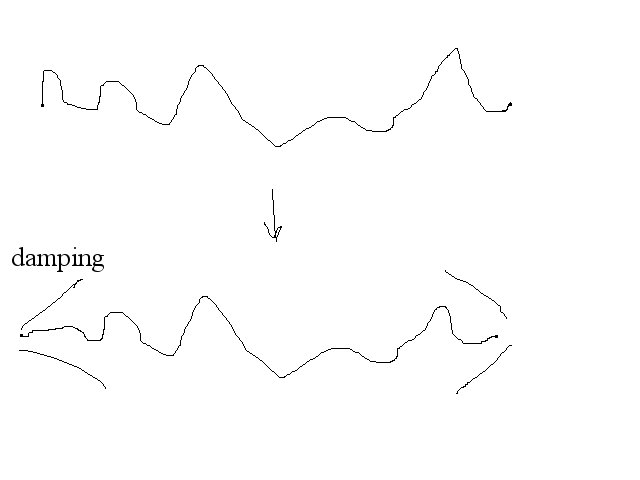
This has an effect on the energy in the string as a whole such that
after a while the motion of the string overall decreases in amplitude,
it makes the virtual string length dependent on the frequency
components which are in it (which is known also to happen in piano
strings), and probably introduces a certain type of (unwanted) linear
distortion to the simulation.
As a result, the string behaves a bit like a normally suspended string
which is also a bit stiff close to the end points, though not
necessarily contractive.
More issues taken into account in the simulator: coupling,
non-linear amplification, feedback
Two more extensions are added to get a good sounding simulation string
instrument, apart from real-time parameter changes; string coupling,
and a overall feedback with non-linear characteristics.
Of course a challenge for this problem which is different from other
simulations is to get a decaying string sound which is rendered as a
sound file over a long simulation interval, for instance a number of
seconds. At CD sample rate, that means hundreds of thousands of
simulation steps, and a noise preferably less then 2^-15 (is less then
0.004 % of maximum amplitude) top to top amplitude.
The simulation software in its various versions also allows research
related work by outputting (also in interaction time) string excursion
and velocity and drawing graphs of these using Tcl/Tk scripts connected
over a socket.
And a real time simulation requires
serious computer horsepower, even
when programmed very efficiently in C.
The quality of the simulation and sound properties
It is possible to use a reflection formula to estimate string motion,
and of course helmholz like standing wave approaches.
In general, the qualities the author was looking for are lost in many
ways by doing so. A lot of the wonderfullness of a sounding string
comes from all the complexities of the physical string and its
interaction with an enclosure and with other strings during the
sounding of a musical chord.
Listen to the demo sounds to get an idea.
home page [2]
email: theover@tiscali.nl [2]




