/* wxMaxima 0.7.2 http://wxmaxima.sourceforge.net
Maxima 5.12.0 http://maxima.sourceforge.net
Using Lisp GNU Common Lisp (GCL) GCL 2.6.8 (aka GCL)
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
This is a development version of Maxima. The function bug_report()
provides bug reporting information.

(%i1) example(sinc);

(%i2) example(commutative);

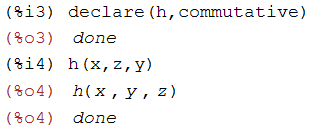
(%i5) integrate(1/(1+x^2));

(%i6) integrate(1/(1+x^2),x);

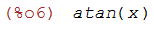
(%i7) integrate(1/(1+x^1),x);

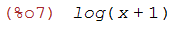
(%i8) integrate(1/(1+x^3),x);

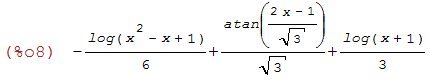
(%i9) -log(x^2-x+1)/6+atan((2*x-1)/sqrt(3))/sqrt(3)+log(x+1)/3;

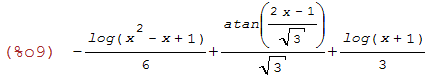
(%i10) taylor(%, x, 0, 8);

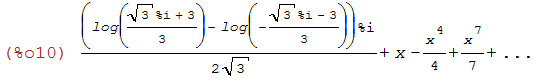
(%i11) ((log((sqrt(3)*%i+3)/3)-log(-(sqrt(3)*%i-3)/3))*%i)/(2*sqrt(3));

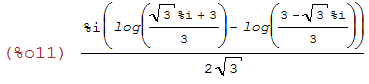
(%i12) ratsimp(%);

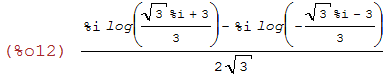
(%i13) radcan(%);

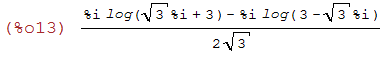
(%i14) factor(%);

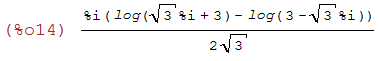
(%i15) expand(%);

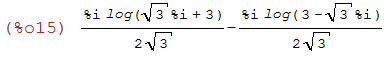
(%i16) trigsimp(%);

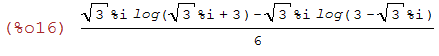
(%i17) trigreduce(%);

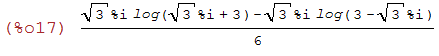
(%i18) wxplot2d([%], [x,-5,5])$

(%i19) float((sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6), numer;

(%i20) if numer#false then numer:false else numer:true;

(%i21) trigreduce(%);

(%i22) (sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6;

(%i23) if numer#false then numer:false else numer:true;

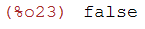
(%i24) gfactor(%);

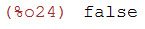
(%i25) gfactor()(sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6);

(%i25) gfactor(sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6);

(%i25) gfactor(sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6);

(%i25) gfactor()(sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6);

(%i25) gfactor()(sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6)));

(%i25) gfactor((sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6);

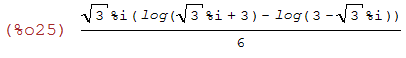
(%i26) if numer#false then numer:false else numer:true;

(%i27) gfactor((sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6);

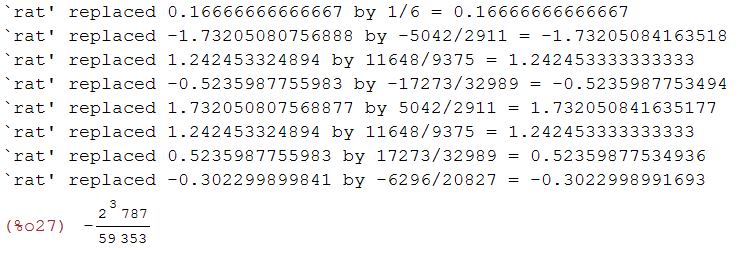
(%i28) if numer#false then numer:false else numer:true;

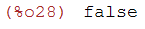
(%i29) gfactor((sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6);

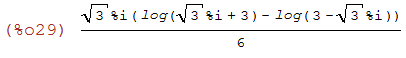
(%i30) gfactor(%);

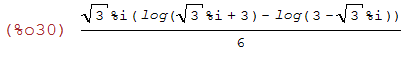
(%i31) radcan(%);

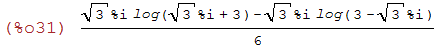
(%i32) rectform(%);

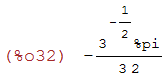
(%i33) polarform(%);

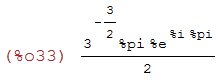
(%i34) rectform((sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6);

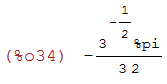
(%i35) rectform((sqrt(3)*%i*log(sqrt(3)*%i+4)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6);

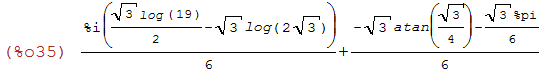
(%i36) taylor((sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6, x, 0, 8);

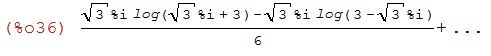
(%i37) if numer#false then numer:false else numer:true;

(%i38) if numer#false then numer:false else numer:true;

(%i39) taylor(-log(x^2-x+1)/6+atan((2*x-1)/sqrt(3))/sqrt(3)+log(x+1)/3, x, 0, 16);

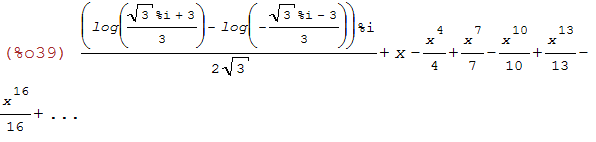
(%i40) taylor(-log(x^2-x+1)/6+atan((2*x-1)/sqrt(3))/sqrt(3)+log(x+1)/3, x, 0, 30);

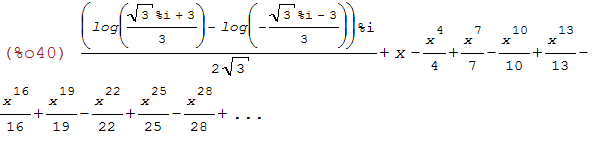
(%i41) taylor(-log(x^2-x+1)/6+atan((2*x-1)/sqrt(3))/sqrt(3)+log(x+1)/3, x, 0, 100);

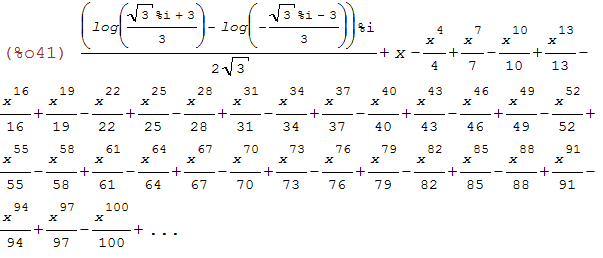
(%i42) rectform(taylor(-log(x^2-x+1)/6+atan((2*x-1)/sqrt(3))/sqrt(3)+log(x+1)/3, x, 0, 100));

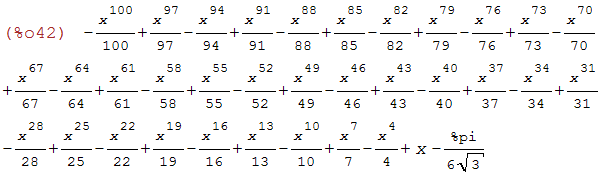
(%i43) rectform(((log((sqrt(3)*%i+3)/3)-log(-(sqrt(3)*%i-3)/3))*%i)/(2*sqrt(3)));

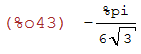
(%i44) rectform((sqrt(3)*%i*log(sqrt(3)*%i+3)-sqrt(3)*%i*log(3-sqrt(3)*%i))/6);

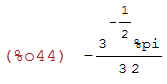
(%i45) integrate(1/(1+x^3),x)-(-x^100/100+x^97/97-x^94/94+x^91/91-x^88/88+x^85/85-x^82/82
 +x^79/79-x^76/76+x^73/73-x^70/70+x^67/67-x^64/64+x^61/61-x^58/58+x^55/55-x^52/52+x^49/49
 -x^46/46+x^43/43-x^40/40+x^37/37-x^34/34+x^31/31-x^28/28+x^25/25-x^22/22+x^19/19-x^16/16
 +x^13/13-x^10/10+x^7/7-x^4/4+x-%pi/(6*sqrt(3)));

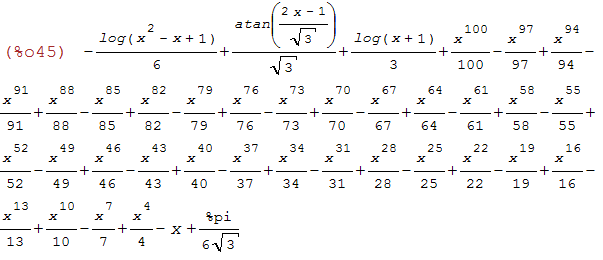
(%i46) plot(%,[x,0,10]);

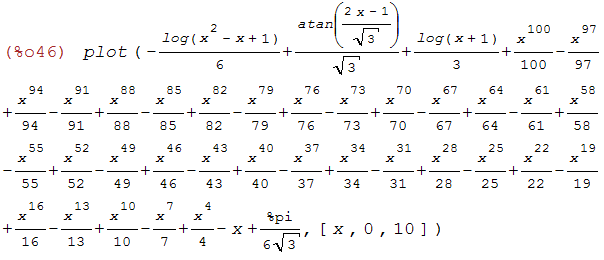
(%i47) plot2d(%,[x,0,10]);

(%i48) integrate(1/(1+x^3),x)-(-x^100/100+x^97/97-x^94/94+x^91/91-x^88/88+x^85/85-x^82/82
 +x^79/79-x^76/76+x^73/73-x^70/70+x^67/67-x^64/64+x^61/61-x^58/58+x^55/55-x^52/52+x^49/49
 -x^46/46+x^43/43-x^40/40+x^37/37-x^34/34+x^31/31-x^28/28+x^25/25-x^22/22+x^19/19-x^16/16
 +x^13/13-x^10/10+x^7/7-x^4/4+x-%pi/(6*sqrt(3)));

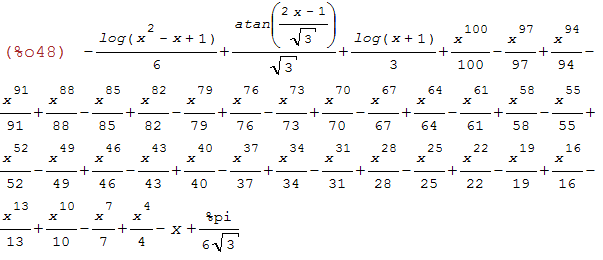
(%i49) plot2d(%,[x,0,10]);

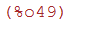
(%i50) integrate(1/(1+x^3),x)-(-x^100/100+x^97/97-x^94/94+x^91/91-x^88/88+x^85/85-x^82/82
 +x^79/79-x^76/76+x^73/73-x^70/70+x^67/67-x^64/64+x^61/61-x^58/58+x^55/55-x^52/52+x^49/49
 -x^46/46+x^43/43-x^40/40+x^37/37-x^34/34+x^31/31-x^28/28+x^25/25-x^22/22+x^19/19-x^16/16
 +x^13/13-x^10/10+x^7/7-x^4/4+x-%pi/(6*sqrt(3)));

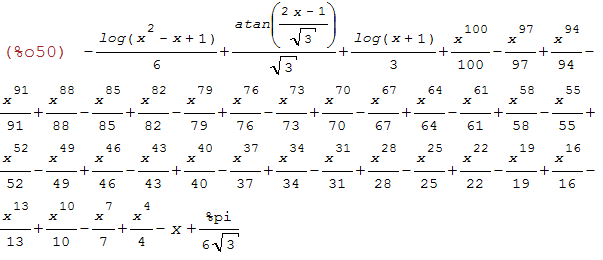
(%i51) plot2d(%,[x,0,1]);
plot2d(integrate(1/(1+x^3),x)-(-x^100/100+x^97/97-x^94/94+x^91/91-x^88/88+x^85/85
 -x^82/82+x^79/79-x^76/76+x^73/73-x^70/70+x^67/67-x^64/64+x^61/61-x^58/58+x^55/55-x^52/52
 +x^49/49-x^46/46+x^43/43-x^40/40+x^37/37-x^34/34+x^31/31-x^28/28+x^25/25-x^22/22+x^19/19
 -x^16/16+x^13/13-x^10/10+x^7/7-x^4/4+x-%pi/(6*sqrt(3))),[x,0,0.8]);

(%i52) fpprec : 32;
plot2d(integrate(1/(1+x^3),x)-(-x^100/100+x^97/97-x^94/94+x^91/91-x^88/88+x^85/85
 -x^82/82+x^79/79-x^76/76+x^73/73-x^70/70+x^67/67-x^64/64+x^61/61-x^58/58+x^55/55-x^52/52
 +x^49/49-x^46/46+x^43/43-x^40/40+x^37/37-x^34/34+x^31/31-x^28/28+x^25/25-x^22/22+x^19/19
 -x^16/16+x^13/13-x^10/10+x^7/7-x^4/4+x-%pi/(6*sqrt(3))),[x,0,0.1]);

(%i53) (%o53)

(%i54) plot2d(integrate(1/(1+x^3),x),[x,0,0.1]);

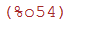
(%i55) (%o55)

(%i56) plot2d(integrate(1/(1+x^3),x),[x,0,10]);

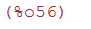
(%i57) plot2d(integrate(1/(1+x^3),x),[x,/1,20]);

(%i57) plot2d(integrate(1/(1+x^3),x),[x,-1,20]);

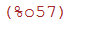
(%i58) plot2d(integrate(1/(1+x^3),x),[x,-10,20]);

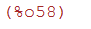
(%i59) log10(x) := log(x) / log(10);

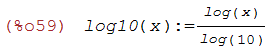
(%i60) f(x):=integrate(1/(1+x^3),x);

(%i61) ft100(x));

(%i61) ft100(x):=x^100/100-x^97/97+x^94/94-x^91/91+x^88/88-x^85/85+x^82/82-x^79/79+x^76/76
 -;

(%i61) ft100(x):=x^100/100-x^97/97+x^94/94-x^91/91+x^88/88-x^85/85+x^82/82-x^79/79+x^76/76
 -
x^73/73+x^70/70-x^67/67+x^64/64-x^61/61+x^58/58-x^55/55+x^52/52-x^49/49+x^46/46-x^43/43
 +x^40/40-x^37/37+x^34/34-x^31/31+x^28/28-x^25/25+x^22/22-x^19/19+
x^16/16-x^13/13+x^10/10-x^7/7+x^4/4-x+%pi/(6*sqrt(3))$

(%i62) ft100(x):=x^100/100-x^97/97+x^94/94-x^91/91+x^88/88-x^85/85+x^82/82-x^79/79+x^76/76
 -
x^73/73+x^70/70-x^67/67+x^64/64-x^61/61+x^58/58-x^55/55+x^52/52-x^49/49+x^46/46-x^43/43
 +x^40/40-x^37/37+x^34/34-x^31/31+x^28/28-x^25/25+x^22/22-x^19/19+
x^16/16-x^13/13+x^10/10-x^7/7+x^4/4-x+%pi/(6*sqrt(3))$

(%i63) ft100(0);

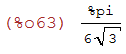
(%i64) fpprec : 32;

(%i65) plot2d(log10(abs(f(x)-ft100(x))),[x,-1,10]);
plot2d(log10(abs(f(x)-ft100(x))),[x,-1,1]);

(%i66) (%o66)

(%i67)