wxMaxima 0.7.4 http://wxmaxima.sourceforge.net
Maxima 5.14.0 http://maxima.sourceforge.net
Using Lisp SBCL 1.0.13
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.

(%i1) exp(-x^2);

(%i2) exp(-x^2);

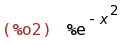
(%i3) plot2d([exp(-x^2)], [x,-5,5],
 [plot_format, gnuplot])$

(%i4) diff(exp(-x^2),x);

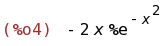
(%i5) plot2d([%o4], [x,-5,5],[plot_format, gnuplot])$

(%i6) diff(exp(-x^2),x,2);

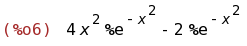
(%i7) plot2d([%o6], [x,-5,5],[plot_format, gnuplot])$

(%i8) taylor(exp(-x^2),x,2);

(%i9) taylor(exp(-x^2),x);

(%i10) taylor(exp(-x^2), x, 0, 4);

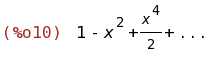
(%i11) integrate(exp(-x^2),x);

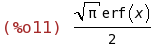
(%i12) integrate(exp(-x^2),x,[-inf,inf]);

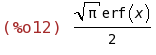
(%i13) integrate(%, x, minf, inf);

(%i14) integrate(%o10, x, minf, inf);

(%i15) integrate(%o10, x, inf);

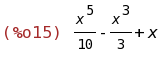
(%i16) integrate(%o02, x, inf);

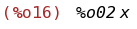
(%i17) integrate(%o2, x, inf);

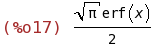
(%i18) integrate(%o2, x, 0, inf);

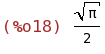
(%i19) integrate(%o2, x, minf, inf);

(%i20) taylor(exp(-x^2), x, 0, 8);

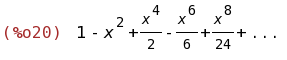
(%i21) integrate(%o20, x, minf, inf);

(%i22) integrate([taylor(exp(-x^2),x)], x, minf, inf);

(%i23) integrate([taylor(exp(-x^2),x,100)], x, minf, inf);

(%i24) integrate([taylor(exp(-x^2))], x, minf, inf);

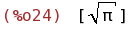
(%i25) integrate([taylor(exp(-x^2),x)], x, minf, inf);

(%i26) integrate([taylor(exp(-x^2),x,100)], x, minf, inf);

(%i27) integrate([taylor(exp(-x^2),x,0,100)], x, minf, inf);

(%i28) integrate([taylor(exp(-x^2),x,0,100)], x, 0, inf);

(%i29) integrate([taylor(exp(-x^2),x,0,200)], x, 0, inf);

(%i30) integrate([taylor(exp(-x^2),x,0,200)], x, 0, 1000);

(%i31) approx(x);

(%i32) approx(%o30);

(%i33) bfloat(integrate([taylor(exp(-x^2),x,0,200)], x, 0, 1000));

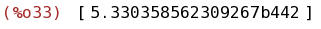
(%i34) bfloat(integrate([taylor(exp(-x^2),x,0,200)], x, -1000, 1000));

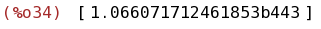
(%i35) bfloat(integrate([taylor(exp(-x^2),x,0,220)], x, -1000, 1000));

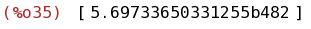
(%i36) bfloat(integrate([taylor(exp(-x^2),x,0,220)], x, -100, 100));

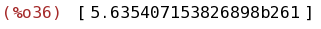
(%i37) bfloat(integrate([taylor(exp(-x^2),x,0,220)], x, -100, 100)-integral(exp(-x^2),x,
 -inf,inf));

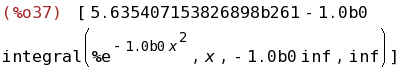
(%i38) bfloat(integrate([taylor(exp(-x^2),x,0,220)], x, -100, 100)-integral(exp(-x^2),x,
 -minf,inf));

(%i39) bfloat(integrate([taylor(exp(-x^2),x,0,220)], x, -100, 100)-integrate(exp(-x^2),x,
 -minf,inf));

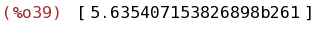
(%i40) bfloat(integrate([taylor(exp(-x^2),x,0,220)], x, -100, 100)-integrate(exp(-x^2),x,0,inf));

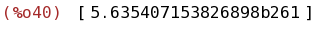
(%i41) bfloat(integrate([taylor(exp(-x^2),x,0,220)], x, -100, 100)-integrate(exp(-x^2),x,minf,inf));

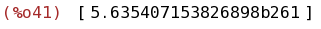
(%i42) bfloat(integrate([taylor(exp(-x^2),x,0,220)], x, -10, 10)-integrate(exp(-x^2),x,minf,inf));

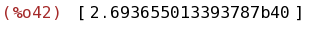
(%i43) float(integrate([taylor(exp(-x^2),x,0,220)], x, -10, 10)-integrate(exp(-x^2),x,minf,inf));

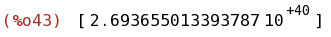
(%i44) float(integrate([taylor(exp(-x^2),x,0,220)], x, -1000, 1000)-integrate(exp(-x^2),x,minf,inf));

(%i45) bfloat(integrate([taylor(exp(-x^2),x,0,220)], x, -1000, 1000)-integrate(exp(-x^2),x,minf,inf));

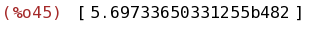
(%i46) bfloat(integrate([taylor(exp(-x^2),x,0,10)], x, -1000, 1000)-integrate(exp(-x^2),x,minf,inf));

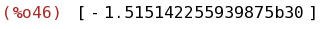
(%i47) bfloat(integrate([taylor(exp(-x^2),x,0,10)], x, -1000, 1000));

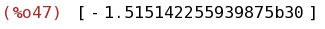
(%i48) bfloat(integrate([taylor(exp(-x^2),x,0,10)], x, -10, 10));

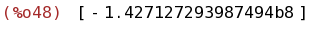
(%i49) bfloat(integrate([taylor(exp(-x^2),x,0,100)], x, -10, 10));

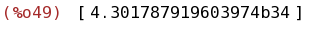
(%i50) taylor(exp(-x^2),x,0,100);

(%i51) integrate(taylor(exp(-x^2),x,0,100),x);

(%i52) integrate(taylor(exp(-x^2),x,0,100),x,0,1);

(%i53) bloat(integrate(taylor(exp(-x^2),x,0,100),x,0,1));

(%i54) bfloat(integrate(taylor(exp(-x^2),x,0,100),x,0,1));

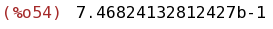
(%i55) bfloat(integrate(taylor(exp(-x^2),x,0,100),x,0,3));

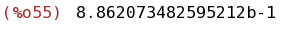
(%i56) bfloat(integrate(taylor(exp(-x^2),x,0,100),x,0,10));

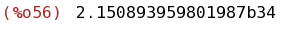
(%i57) bfloat(integrate(taylor(exp(-x^2),x,0,1000),x,0,10));

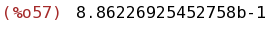
(%i58) plot2d([integrate(taylor(exp(-x^2),x,0,1000),x,0,10))], [x,-5,5],
 [plot_format, gnuplot])$

(%i58) plot2d([integrate(taylor(exp(-x^2),x,0,1000),x,0,10)))], [x,-5,5], [plot_format, gnuplot]);

(%i58) plot2d([integrate(taylor(exp(-x^2),x,0,1000),x,0,10)), [x,-5,5], [plot_format, gnuplot]);

(%i58) plot2d([integrate(taylor(exp(-x^2),x,0,1000),x,0,10))], [x,-5,5], [plot_format, gnuplot]);

(%i58) plot2d([integrate(taylor(exp(-x^2),x,0,1000),x,0,10)], [x,-5,5], [plot_format, gnuplot]);

(%i59) plot2d([integrate(taylor(exp(-x^2),x,0,1000),x,0,x)], [x,0,5], [plot_format, gnuplot]);

(%i60) plot2d([integrate(taylor(exp(-x^2),x,0,100),x,0,x)], [x,0,5], [plot_format, gnuplot]);

(%i61) plot2d([integrate(taylor(exp(-x^2),x,0,100),x,0,x)], [x,0,1], [plot_format, gnuplot]);

(%i62) plot2d([integrate(taylor(exp(-x^2),x,0,200),x,0,x)], [x,0,1], [plot_format, gnuplot]);

(%i63) plot2d([integrate(taylor(exp(-x^2),x,0,200),x,0,x)], [x,0,2], [plot_format, gnuplot]);

(%i64) plot2d([integrate(taylor(exp(-x^2),x,0,200),x,0,x)], [x,0,3], [plot_format, gnuplot]);

(%i65) plot2d([integrate(taylor(exp(-x^2),x,0,200),x,0,x)], [x,0,4], [plot_format, gnuplot]);

(%i66) plot2d([integrate(taylor(exp(-x^2),x,0,200),x,0,x)], [x,0,5], [plot_format, gnuplot]);

(%i67) plot2d([integrate(taylor(exp(-x^2),x,0,200),x,0,x) -integrate(exp(-x^2),x,0,x) ],
  [x,0,5], [plot_format, gnuplot]);

(%i68) integrate(exp(-x^2),x,0,5);

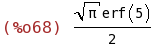
(%i69) bfloat(%);

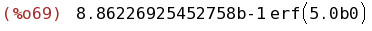
(%i70) float(%), numer;

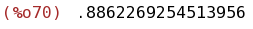
(%i71) bfloat(integrate(exp(-x^2),x,0,5));

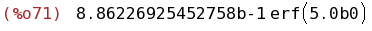
(%i72) float(integrate(exp(-x^2),x,0,5));

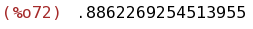
(%i73) bfloat(integrate(exp(-x^2),x,0,5));

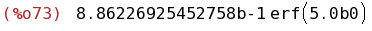
(%i74) bfloat(integrate(exp(-x^2),x,0,5),16);

(%i75) tofloat(integrate(exp(-x^2),x,0,5),16);

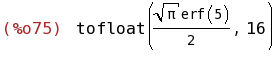
(%i76) if numer#false then numer:false else numer:true;

(%i77) bfloat(integrate(exp(-x^2),x,0,5));

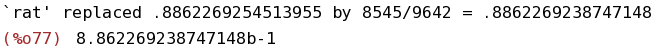
(%i78) integrate(taylor(exp(-x^2),x,0,200),x,0,4) -integrate(exp(-x^2),x,0,4);

(%i79) integrate(taylor(exp(-x^2),x,0,200),x,0,5) -integrate(exp(-x^2),x,0,5);

(%i80) if numer#false then numer:false else numer:true;

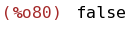
(%i81) integrate(taylor(exp(-x^2),x,0,200),x,0,5) -integrate(exp(-x^2),x,0,5);

(%i82) bfloat(%);

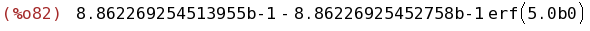
(%i83) float(%);

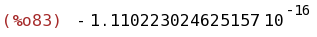
(%i84) float(integrate(taylor(exp(-x^2),x,0,200),x,0,4) -integrate(exp(-x^2),x,0,4));

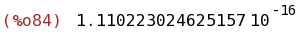
(%i85) float(integrate(taylor(exp(-x^2),x,0,200),x,0,1) -integrate(exp(-x^2),x,0,1));

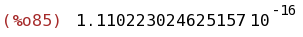
(%i86) fpprec : 20;

(%i87) float(integrate(taylor(exp(-x^2),x,0,200),x,0,1) -integrate(exp(-x^2),x,0,1));

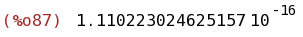
(%i88) float(integrate(taylor(exp(-x^2),x,0,200),x,0,4) -integrate(exp(-x^2),x,0,4));

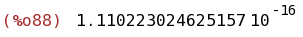
(%i89) float(integrate(taylor(exp(-x^2),x,0,200)-exp(-x^2),x,0,4));

(%i90) integrate(taylor(exp(-x^2),x,0,200)-exp(-x^2),x,0,4);

(%i91) if numer#false then numer:false else numer:true;

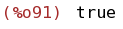
(%i92) if numer#false then numer:false else numer:true;

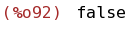
(%i93) integrate(taylor(exp(-x^2),x,0,20)-exp(-x^2),x,0,4);

(%i94) plot2d([taylor(exp(-x^2),x,0,200)-exp(-2^x)], [x,0,5], [plot_format, gnuplot]);

(%i95) plot2d([taylor(exp(-x^2),x,0,20)-exp(-2^x)], [x,0,5], [plot_format, gnuplot]);

(%i96) plot2d([taylor(exp(-x^2),x,0,200)-exp(-2^x)], [x,0,4], [plot_format, gnuplot]);

(%i97) plot2d([taylor(exp(-x^2),x,0,50)-exp(-2^x)], [x,0,4], [plot_format, gnuplot]);

(%i98) plot2d([taylor(exp(-x^2),x,0,100)-exp(-2^x)], [x,0,4], [plot_format, gnuplot]);

(%i99) plot2d([taylor(exp(-x^2),x,0,150)-exp(-2^x)], [x,0,4], [plot_format, gnuplot]);

(%i100) plot2d([taylor(exp(-x^2),x,0,150)-exp(-x^2)], [x,0,4], [plot_format, gnuplot]);

(%i101) plot2d([taylor(exp(-x^2),x,0,200)-exp(-x^2)], [x,0,5], [plot_format, gnuplot]);

(%i102) plot2d([taylor(exp(-x^2),x,0,20)-exp(-x^2)], [x,-5,5], [plot_format, gnuplot]);

(%i103) plot2d([taylor(exp(-x^2),x,0,10)-exp(-x^2)], [x,-5,5], [plot_format, gnuplot]);

(%i104) plot2d([taylor(exp(-x^2),x,0,1)-exp(-x^2)], [x,0,1], [plot_format, gnuplot]);

(%i105) plot2d()-exp(-x^2)], [x,0,1], [plot_format, gnuplot]);

(%i105) plot2d([-exp(-x^2)], [x,0,1], [plot_format, gnuplot]);

(%i106) plot2d([(taylor(exp(-x^2),x,0,10))-exp(-x^2)], [x,-5,5], [plot_format, gnuplot]);

(%i107) plot2d([taylor(exp(-x^2),x,0,10)], [x,-5,5], [plot_format, gnuplot]);

(%i108) plot2d([taylor(exp(-x^2),x,0,100)], [x,-5,5], [plot_format, gnuplot]);

(%i109) plot2d([taylor(exp(-x^2),x,0,200)], [x,-4,4], [plot_format, gnuplot]);

(%i110) maxtayorder:false;

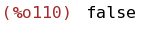
(%i111) plot2d([(taylor(exp(-x^2),x,0,10))-exp(-x^2)], [x,-5,5], [plot_format, gnuplot]);

(%i112) maxtayorder:true;

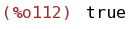
(%i113) plot2d([(taylor(exp(-x^2),x,0,10))-exp(-x^2)], [x,-5,5], [plot_format, gnuplot]);

(%i114) plot2d([taytorat((taylor(exp(-x^2),x,0,10)))-exp(-x^2)], [x,-5,5], [plot_format, gnuplot]);

(%i115) plot2d([taytorat((taylor(exp(-x^2),x,0,100)))-exp(-x^2)], [x,-5,5], [plot_format,
  gnuplot]);

(%i116) plot2d([taytorat((taylor(exp(-x^2),x,0,200)))-exp(-x^2)], [x,-4,4], [plot_format,
  gnuplot]);

(%i117)