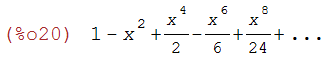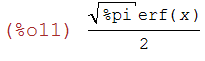Theo Verelst Local Diary Page 63


I've ditched the usual header for the moment, I think it doesn't help much anyhow.
This page is copyrighted by me, and may be read and transfered by any means only as a whole and including the references to me. I guess thats normal, the writer can chose that of course, maybe I´ll make some creative commons stuff one day, of course I have made Free and Open Source software and even hardware designs available!

Home (alt)   Tripod Home   Local Diary list   Tripod Diary List   Previous Diary

This page is under contruction, so check back later, too.

  Mon Dec 29 12:54, 2008

Of course you don't NEED to use an full HD screen to view this page, but it sure helps...

90s hits?

"When I'm walking through a shadow of Death and take a look at my life..."


   

   Billboard Hot 100 (1995)


   Billboard Hot 100 (1998)



Awfull.

A CUDA accelerated Cinelerra plugin


PPM 256
ICC profiles / prefs

After solving more than a handfull of bugs I had cinepaint running from my own compilation.

The next thing after having compiled, added to and analysed here and there the Cuda examples should be I thought to add some Cuda processing to a slow plugin.

See also the NVidia Cuda forum. 



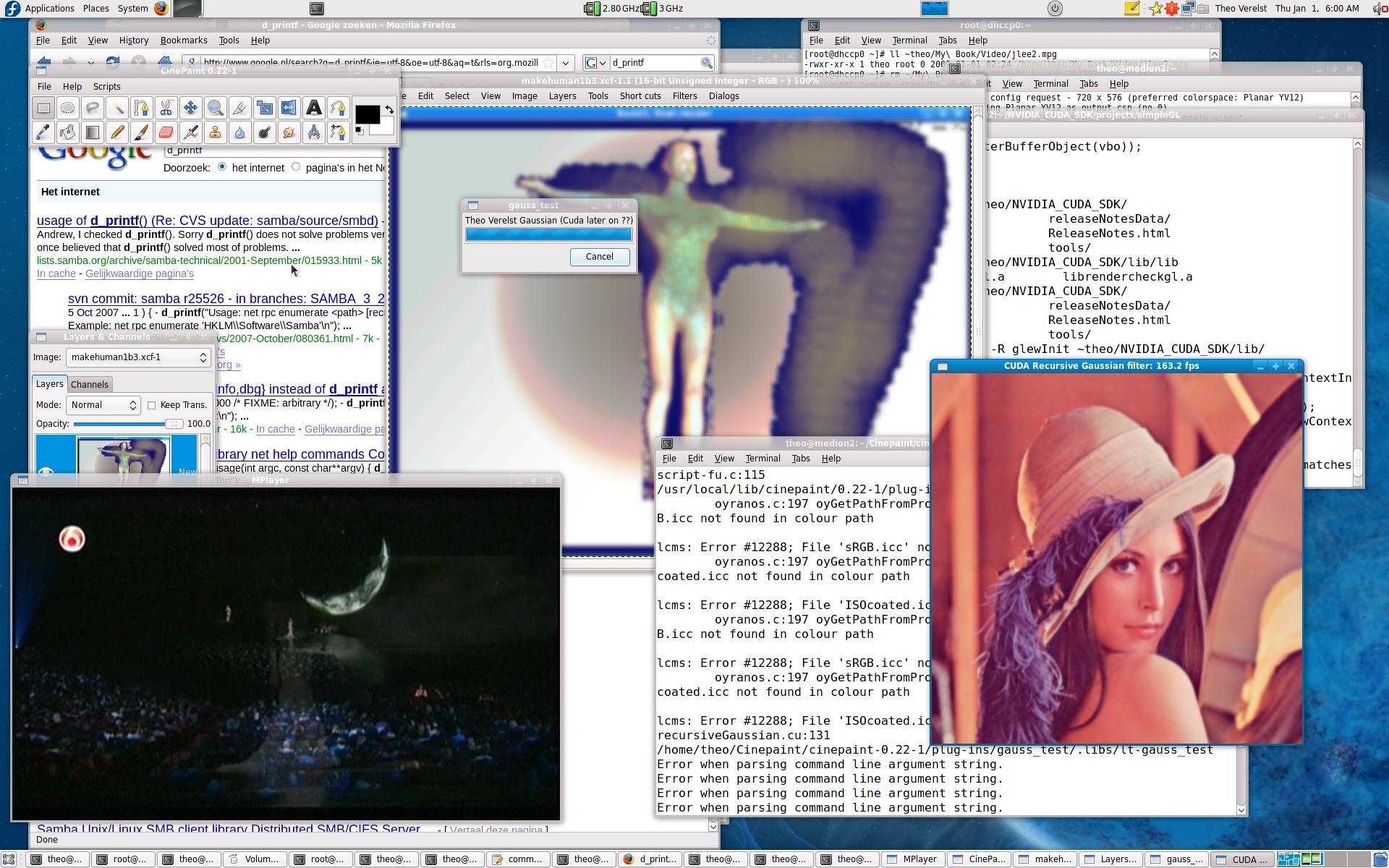
    The first (actually) Cuda Cinepaint plugin ttyout screendump


The working Gaussian Blur Cuda plugin in Cinepaint:



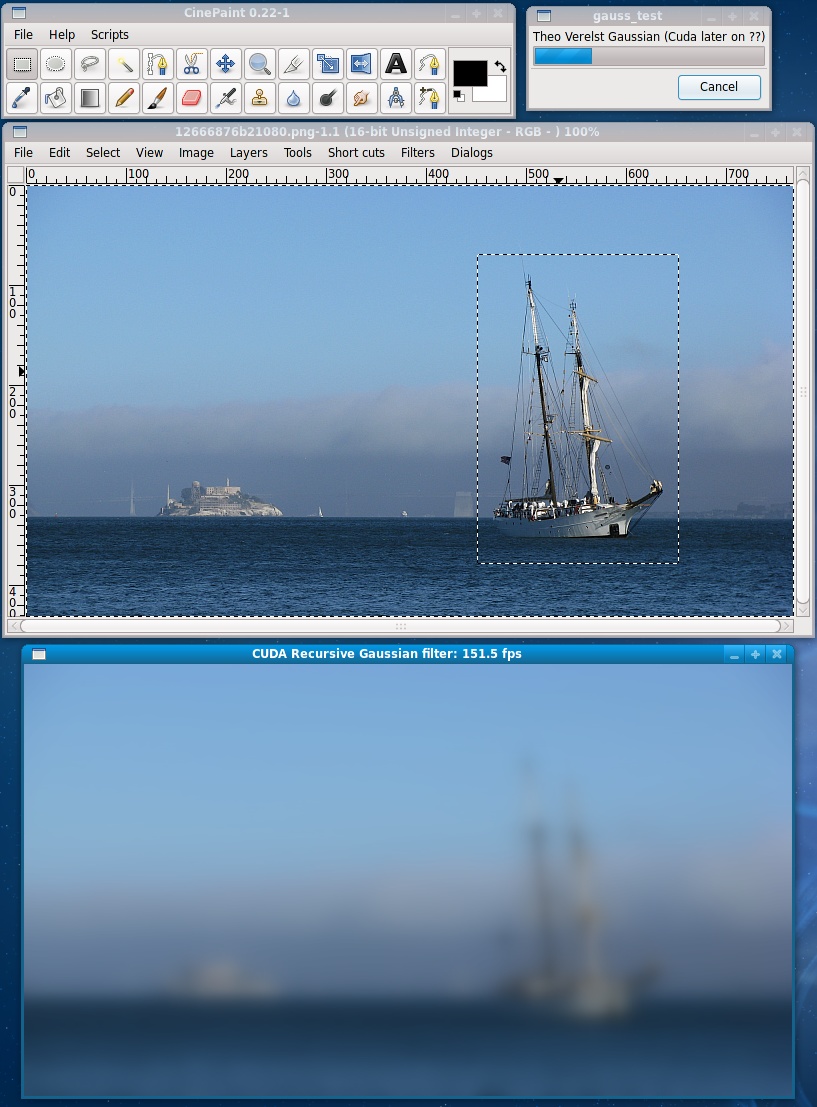
Is that 151.5 FRAMES PER SECOND ?! It is...

The result:









More compile work




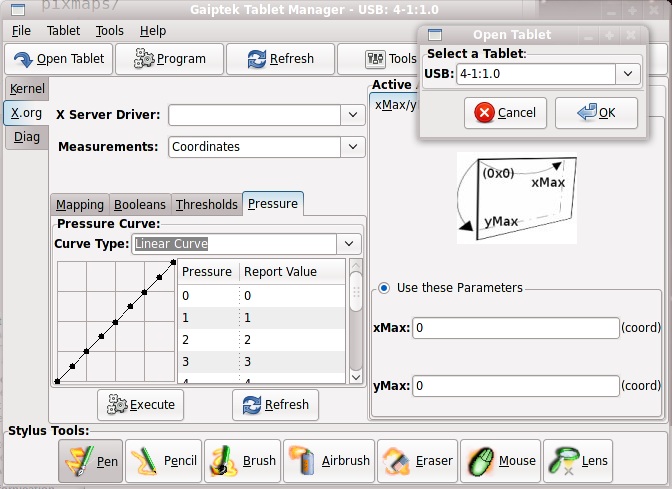
This don't compile/work on Fedora 10/64, Theo! Tell me about it, but after many hours, this developer can make it so. But, now the X driver needs work to talk nicely with it. Grrr.

Math for years of hand-computation

This was EE first year material in 1984 (magical year) at DUT when elektisch was maybe still electrisch, I don't remember, but it was just after the curriculum had been made into university level instead of 'hogeschool'  which was kind enhanced bachelor level.

Taylor expansion means a differentiable function is replaced by a sum of a number of polynomial terms, up til a certain degree, which are computed by approximating a number of derivatives of the function at that point. See mathematical literature for the rifht formulas. For engineers such expansion is usefull because it is a good approximation and the next term of the expansion of a certain degree is a upper bound for the error, under certain strict conditions, which makes it a good approximating expansion because it also is fairly stable and usable for many physically oriented applications.

Here are some Maxima formulas and the result of giving them to that package as assignment.

First a tryout of the taylor row of the 8th degree from Maxima:


   taylor(exp(-x^2), x, 0, 8);


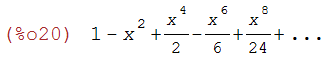
In fact it remembers its an expansion, but it only show the first 8 degree terms.

An important function in Physics and statistics is the gaussian, which is not easy to integrate but maxima can do a formal integration with filled in boundaries. Here is the formal integral with a built in function (exercise: fill in the boundaries):

   integrate(exp(-x^2),x);



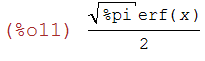
Now I take a 200 (very many) degree taylor expansion of the gaussian and integrate the Taylor expansion, which is possible because it's a 200 degree polynomial of even a decent form:

   integrate([taylor(exp(-x^2),x,0,200)], x, 0, 1000);


Notice that equalling fractions by maxima and working with 'infinite'  precision numbers makes the resulting fraction which aproximates the above integral have more than 500 digits!

See below for a 100 term expansion (without integrating) in a smaller form:

   taylor(exp(-x^2),x,0,100);



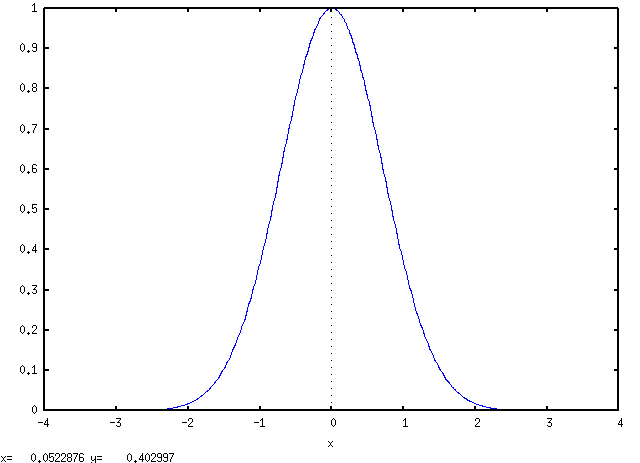
This is a plot of the taylor expansion of the gaussian around 0:

   plot2d([taylor(exp(-x^2),x,0,200)], [x,-4,4], [plot_format, gnuplot]);



And of the derivative of the actual gaussian:




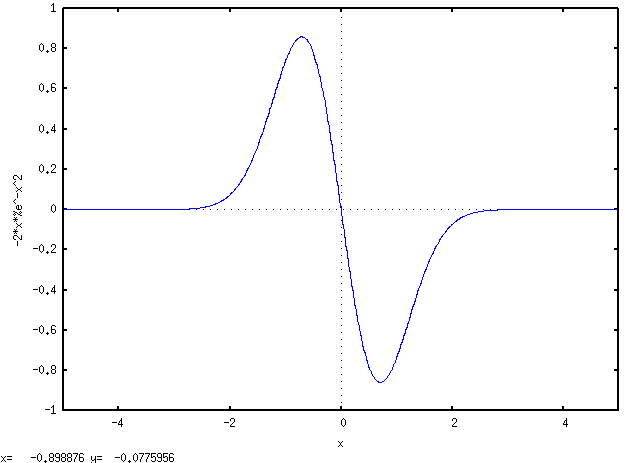
Now a plot of the difference between the gaussian and its 100th order taylor expansion, plotting the approximation error between -5 and +5:

   plot2d([taytorat((taylor(exp(-x^2),x,0,100)))-exp(-x^2)], [x,-5,5], [plot_format, gnuplot]);



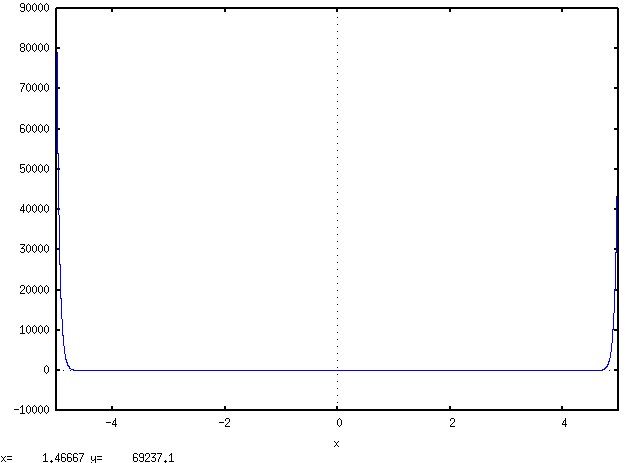
We can see the approximation suddenly becomes very inaccurate above 4.7.

If we scale that graph down to look at the small errors when this begins, we get for a 200 degree appoximation:

   plot2d([taytorat((taylor(exp(-x^2),x,0,200)))-exp(-x^2)], [x,-4,4], [plot_format, gnuplot]);





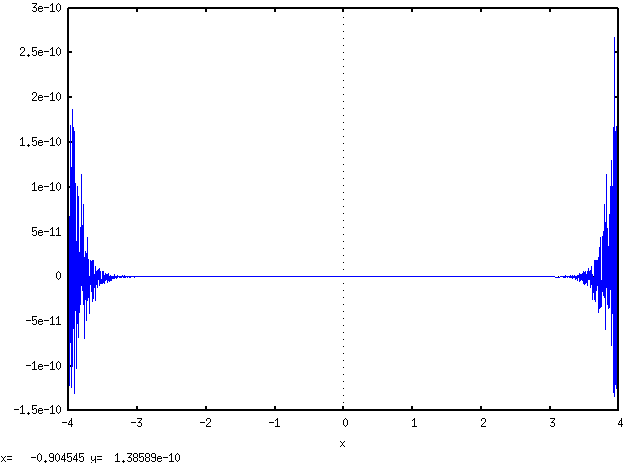
But is this the result we're looking for ?! Where does the rounding take place? Those are important questions I worked on.


The Guitar Rack of Choise ?




rakarrack 0.2.0 - Copyright (c) Daniel Vidal - Josep Andreu - Hernan Ordiales

Heaeaeavvvyyy!